Lõpuks viimane postitus selles tsüklis. Kannatamatud võivad kohe kerida postituse lõppu, teised on teretulnud lugema teksti allpool.
Practical Hydrography
Õppejõud: professor Maxim van Norden
Credit hours: 2
Õpik: How to Read a Nautical Chart by Nigel Calder ($8,34). See on mingi raamat nohikutest paadimeestele, ei saa üldse aru mis ta siin teeb
Õppeprotsess: on huvitav. Põhjalikud loengud, saan teada palju uut ja kasulikku. HYPACK tarkvara installitud läpakatesse ja mille USB-võti tuleb hoida nagu silmatera. Juba on olnud päris mõõdistamine jões ühekiirelise kajaloodiga (sellest tuleb eraldi postitus). Ja tuleb veel, järjest keerulisema tehnikaga.
Iseseisvad tööd: raamatu lugemine. Kirjalikud kodused tööd kuskil 10 küsimusega/ülesandega igaüks. Aruanne kirjutamine ülalmainitud mõõdistamise kohta.
Van Norden räägib IHO struktuurist
Tahvlil – laevakuju loomine HYPACK-is
Esimene praktiline ülesanne selles aines
KONKURSS!
Seda võtmepaela saab esimene õigesti vastanu. Kui mitte keegi ei vasta õigesti s.t. 1 sõlme täpsusega, siis auhinda ei anta. Auhinna üleandmisega võib minna aega, aga ma luban, et see jõuab võitjani.
Merepõhjas asuvad 2-meetrised objektid. Ühe sellise objekti kindlaks avastamiseks on vaja vähemalt 5 peegeldunud signaali objektilt. Milline on sellisel juhul mõõdistuslaeva maksimaalne lubatud kiirus (sõlmedes) kui ühekiirelise sonari maksimaalne impulssite sagedus on 20 ping/s, kiire nurk 8 kraadi, veesügavus 100m ja põhi on tasane.
Kasuks tuleb, kui oma vastusele lisate kirjelduse kuidas selleni jõudsite.
Õige vastus avaldatakse 48 tunni pärast, 27. septembril 2018 siin samas postituse lõpus.
VÕITJAT EI SELGUNUD, VASTUS ASUB ALLPOOL
KERI
KERI VEEL
Vastus:
Kõigepealt tuleb arvutada maksimaalne pingimise sagedus antud sügavusel järgmise valemi abil: C/z*2, kus C on helikiirus (antud juhul 1500 m/s) ja z on sügavus. Tuleb välja, et 1500/100*2 = 7,5 ping/s.
Edasi kasutame valemi maksimaalse pingimise sageduse arvutamiseks MPR = (V*N) / 2*z*tan(a/2)*1,944*S, kus a on kajaloodi kiire nurk, V – laevakiirus sõlmedes, S – otsitava objekti suurus ja N – peegelduste arv.
Sellest valemist arvutame välja V = (MPR*2*z*tan(a/2)*1,944*S) / N = umbes 81 sõlme.
Järelkult, niikaua kui mõõdistusaluse kiirus ei ületa 81 sõlme, võib saada 2-meetrilistelt objektidelt vähemalt 5 peegeldust.
A Middle-aged Hydrographer's Notebook 
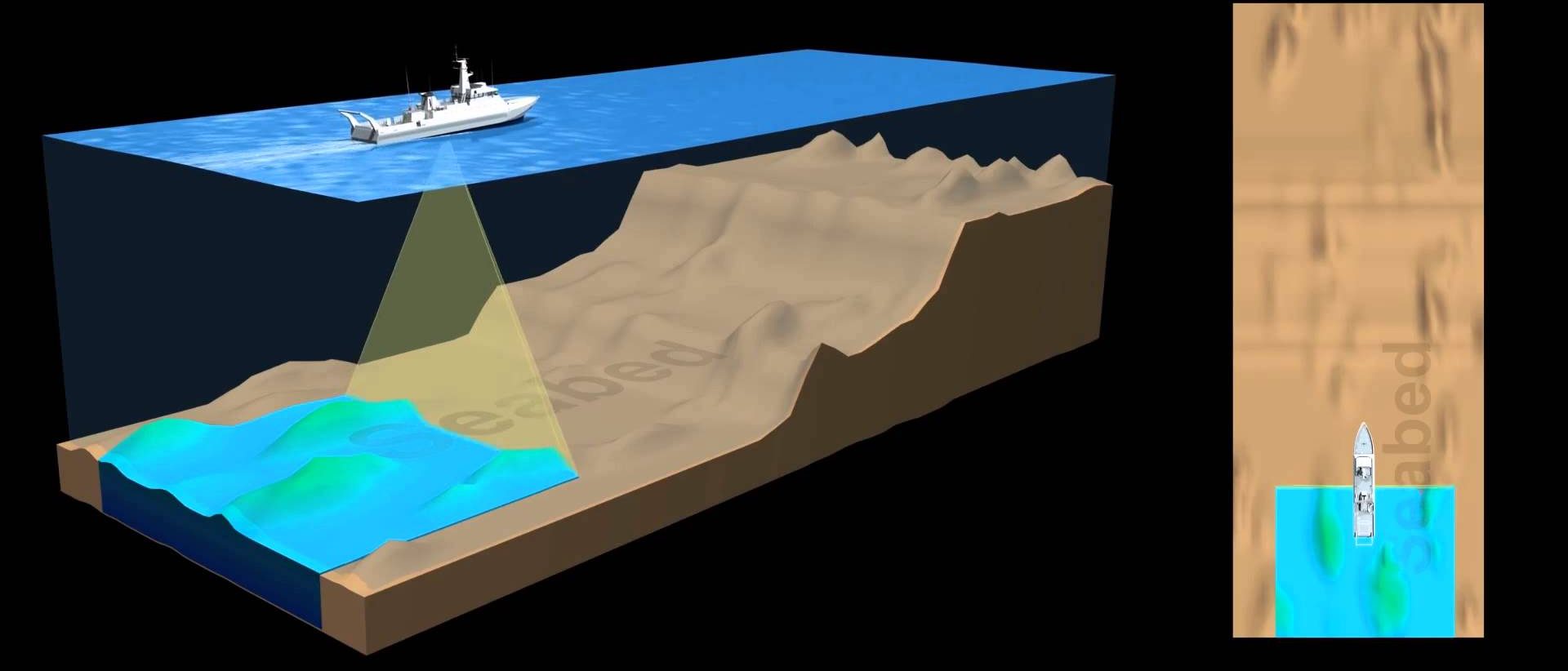
Kust tuleb 1.944 koef?
LikeLike
See koeffitsient käib valemiga koos ja on vajalik selleks, et kasutada samas valemis kiirus sõlmedes ja objekti suurus meetrites.
LikeLike
Nõrk, lahenduskäik näitamata, lihtsalt mingi valem võetud ja numbrid sissepandud.
Kuna 81 sõlme tundus ulme number olevat, siis toon oma lahenduskäigu. Doktrorant kiitis heaks.
Kajaloe jälg 100m sügavuses vees tan8*100 = 14m
Kui laev liigub, siis sonar “näeb” 2m objekti (ette,objekti kohal+taha) 14/2+2+14/2 = 16m jooksul
Eeldusel, et laev liigub ühtlaselt 16m/5pingi = 3.2m max pingide vahe
Üheks pingiks kulub, eeldusel helikiirus vees 1500m/s (100m+100m)/1500m/s=0.13s
Maksimaalne laeva liikumise kiirus on 3.2m/0.13s=24.61m/s ehk 47.84sõlme
Mis arvad sellest?
LikeLike
Kõigepealt, ma arvan et teie oleksite pidanud avaldama oma lahendust õigel ajal.
Teiseks, minul on lahenduskäik olemas ja see koosnebki spetsiaalsest valemist mis on selleks ettenähtud.
Kolmandaks, te saite valesti aru küsimusest. Maksimaalne kiirus antud juhul tähendab kiirust millest kiiremini mõõdistades enam ei suudeta katta objekti 5 pingiga. Kõik kiirused allpool seda on samuti ok. Ja kui minu 81 sõlm on “ulme”, siis kuidas teie poolt arvutatud 47 on reaalsem number?
Neljandaks, teie lahenduses on viga selles osas
14/2+2+14/2
Kuidas teil objekti ette ja taha langeb pool jälje ehk 7m, aga objekti kohal jälg on järsku 2m? Objekti kohal on jälg 14.
Viiendaks, geodeesia doktorandi pädevusest hüdrograafias ma parem ei räägi.
LikeLike
Enda arust sain küsimusest õieti aru. Googlit ja käsiraamatuid ei kasutanud, oma pea ainult.
Kuna anduri kiirgamise ja vastuvõtmise nurk on 8kraadi, siis “näeb” merepõhja andurist ettepoole 7m ja kui laev liigub objektist mööda tahapoole 7m, kui põhi on andurist 100m kaugusel. Pluss liigume objekti kohal 2m. Kokku tulebki 16m. Right?
Kuskohast sa said MPR valemi?
LikeLike
Valem on õpikust. Hea, et üritasid ilma selleta hakkama, aga nüüd tead paremat teed.
LikeLike
Mõningad täpsustused Petsi arvutusmetoodikasse:
1. trigonomeetria (tan(8/2)*100)*2=13,985362 (komakohad annavad lõpptulemusse märgatava muutuse)
Seega esimese ja viienda pingi vahele ei tohi jääda rohkem kui 15,985362 meetrit.
2. esimese ja viienda pingi vahele jääb kolm pingi ja neli(!) pingide vahedistantsi
seega 15,985362/4=3,996341 max distants kahe pingi vahele
3. ühe pingi ajakulu täpsemalt oleks 0,1333333333333333333333333333333333333333333333333333 s
Lõppkokkuvõtteks maksimaalne kiirus: 29,9725 m/s = 58,26 sõlme.
***********************************************************************
IHO “Manual On Hydrography”
on selline valem (lk. 213):
V =(L+Bw) / ((N-1)*t)
kus:
L – objekti pikkus (käesolevas ülesandes 2 m)
Bw (Beam width) – kajaloodi kiire laius merepõhjas (13,985362 m)
N – nõutavate pingide arv (5)
t – pingide ajaline vahe (0,1333333333333333333333333333333333333 s)
Kokku:
V = 29,9725 m/s = 58,26 sõlme
LikeLike
Nõus, aga sinu esimene valem oli BS.
Mina eksisin, laev peab läbima 4 pingi distantsi, mitte 5.
LikeLike
Eelmise kommi parandus,
Kirilli esitatud valem on BS.
LikeLike